概要¶
- トピックモデル(特に、Latent Dirichlet Allocation (LDA))
- 変分ベイズ法による推論
- 実装
トピックモデルでやりたいこと¶
文書集合が与えられた時に、 トピック に応じて文書分類をしたい。
- 文書1=「台風24号が関東に接近します。最大風速は....」
- 文書2=「台風24号の影響で野球が中止に。」
- 文書3=「テニス選手の○○が全英オープンで初優勝しました。」
- 文書4=「○○教授がノーベル生理学・医学賞受賞。」
トピックモデルの重要な仮定(1/3)¶
トピックが異なると使われる単語が異なる。
- 例1. 「テニス」という単語は、スポーツ記事以外ではあまり出現しない。
- 例2. 「台風」という単語は、気象の記事以外ではあまり出現しない。
- 例3. どのトピックでも出現する単語もある(「が」とか)
トピックモデルの重要な仮定(2/3)¶
ひとつの文書には複数のトピックが含まれうる
- 文書1 = 天候100%
- 文書2 = 天候50%、スポーツ50%
- 文書3 = スポーツ100%
- 文書4 = 科学100%
トピックモデルのなんとなくの説明¶
各トピックごとに異なる単語分布を持っている
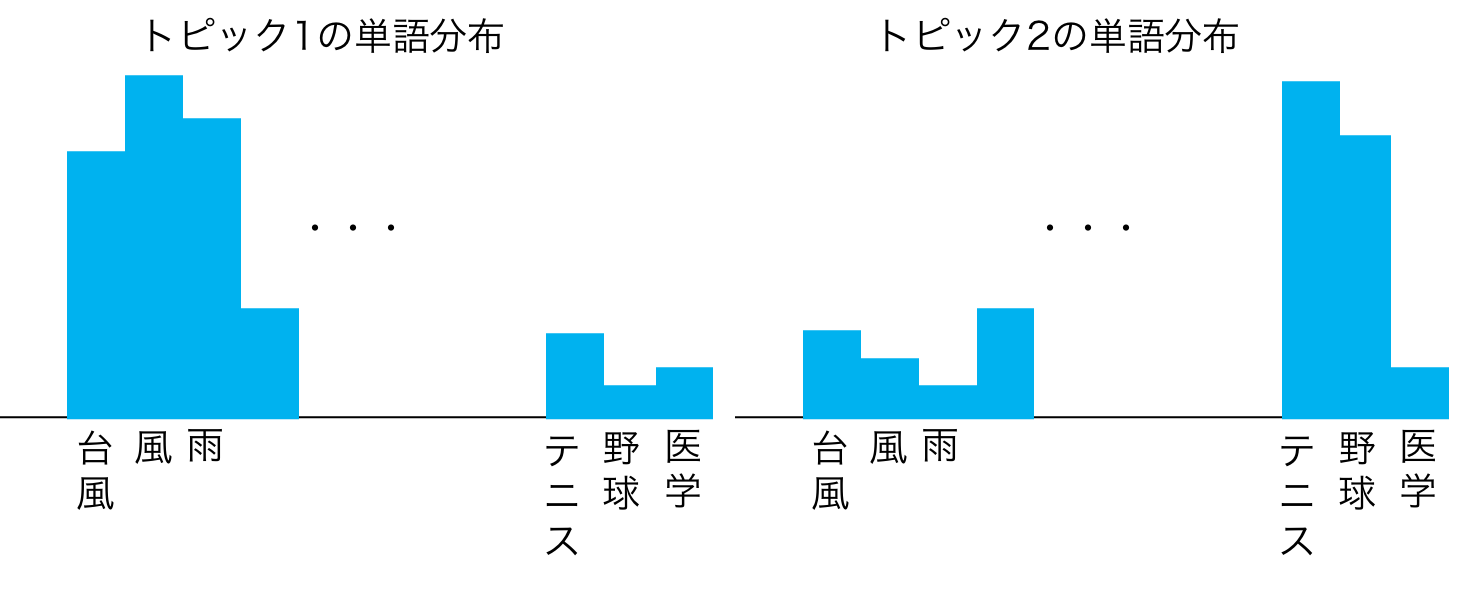
トピックモデルのなんとなくの説明¶
各文書はトピック分布で特徴付けられる
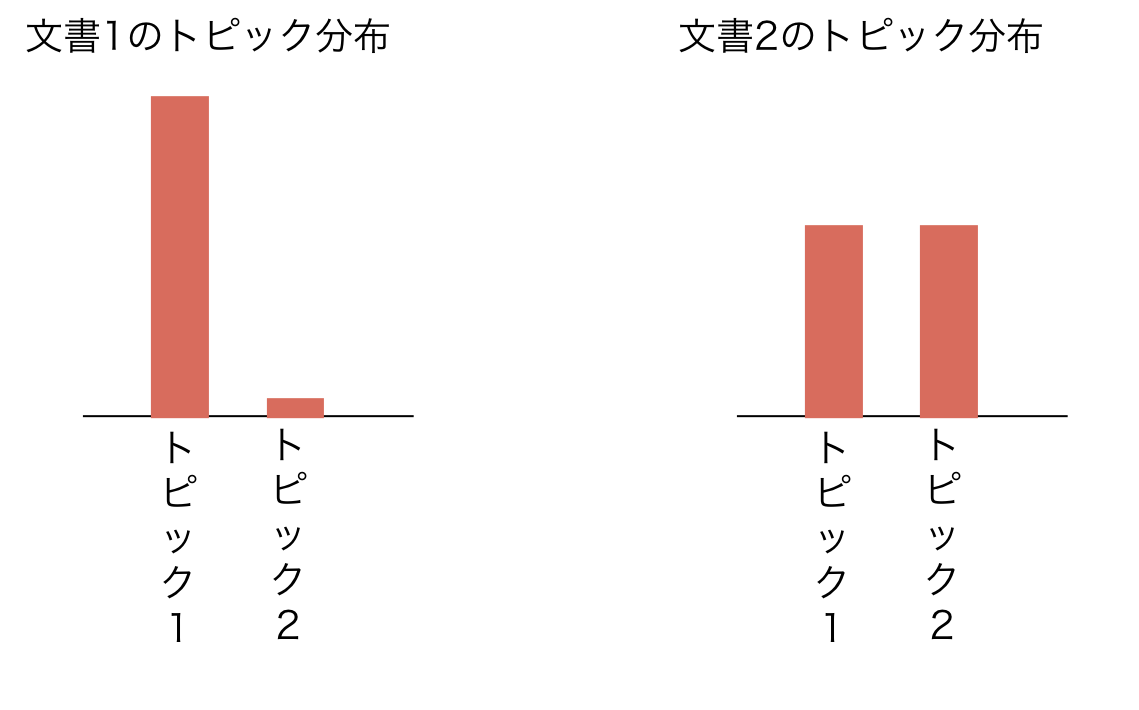
トピックモデルのなんとなくの説明¶
トピック分布からトピックを決め、そのトピックの単語分布から単語をサンプリングすることを繰り返して文書を作る。
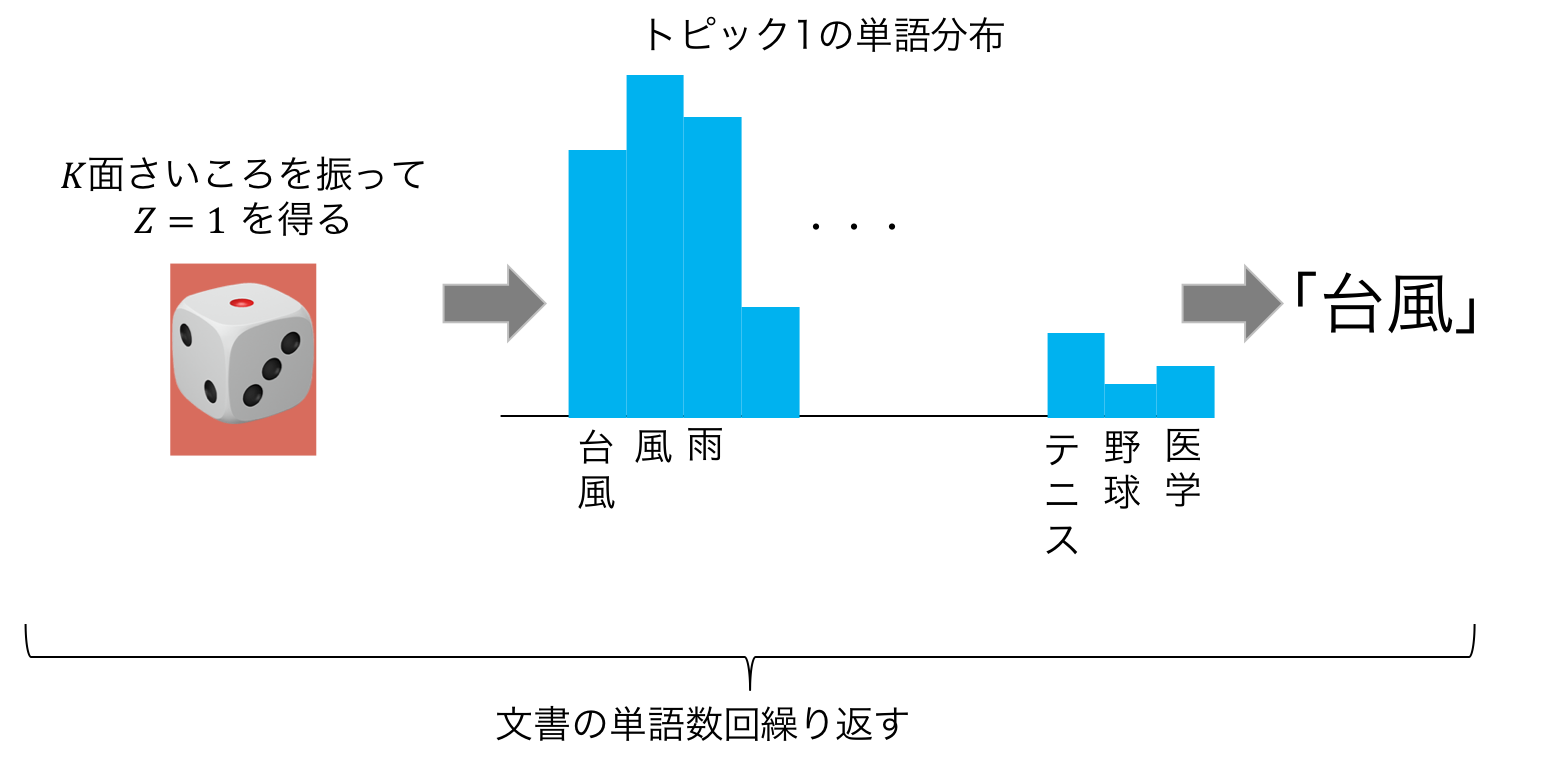
数学的な表現への準備¶
データの表現
- 文書集合 $w=\{{w}_1,{w}_2,\dots,{w}_M\}$
- 文書 $w_m = [w_{m,1}, \dots, w_{m,N_m}]$ $(m=1,\dots,M)$
- 単語 $w_{m,n}\in\{1,\dots,V\}$
以下用いる記法¶
添字が省略されている際には、その添字の範囲を全て含むベクトル・行列を表すものとする
- $\beta_{k,v}$ は $k=1,\dots,K,\ v=1,\dots,V$ の範囲で定義されている
- $\beta_{k} = \begin{bmatrix}\beta_{k,1} & \beta_{k,2} & \dots & \beta_{k,V}\end{bmatrix}$
- $\beta = \begin{bmatrix}\beta_{1,1} & \beta_{1,2} & \dots & \beta_{1,V} \\ \beta_{1,1} & \beta_{1,2} & \dots & \beta_{1,V} \\ & & \vdots & \\ \beta_{K,1} & \beta_{K,2} & \dots & \beta_{K,V} \end{bmatrix}$ など
数学的な表現への準備(例)¶
- 単語集合 $\{1,\dots,6\}=\{\mathrm{a, is, dog, cat, walking, sleeping}\}$
- 文書1 ${w}_1=[\mathrm{a, dog, is, walking}]=[1,3,2,5]$
- 文書2 ${w}_2=[\mathrm{a, cat, is, sleeping}]=[1,4,2,6]$
- 文書集合 $w=\{{w}_1, {w}_2\}$
モデル(1/3)¶
- 文書 $m$ のトピック分布のパラメタ $\theta_m=\begin{bmatrix}\theta_{m,1} & \dots & \theta_{m,K}\end{bmatrix}\in\Delta^{K-1}$
- ディリクレ分布に従う
- $\theta_{m,k}\geq0$, $\sum_{k=1}^K \theta_{m,k} = 1~(m=1,\dots,M)$ が必ず成り立つ $$ \begin{array} \ &p(\theta_{m} \mid \alpha) = \mathrm{Dir}(\theta_m; \alpha) = \dfrac{\Gamma(\sum_{k=1}^K \alpha_k)}{\prod_{k=1}^K\Gamma(\alpha_k)} \prod_{k=1}^K \theta_{m,k}^{\alpha_k-1}~(\alpha_k>0) \end{array} $$
モデル(2/3)¶
- 文書 $m$ の $n$ 個目の単語に紐づくトピック $z_{m,n}\in\{1,\dots,K\}$
- パラメタ $\theta_m$ のCategorical distributionに従う $$ \begin{array} \ &p(z_{m,n}=k \mid \mathbf{\theta}_m) = \theta_{m,k}\\ \text{where} & \sum_{k=1}^K \theta_{m,k} = 1~(m=1,\dots,M) \end{array} $$
モデル(3/3)¶
- 単語数$=V$, トピック数$=K$.
- 文書 $m$ の $n$ 個目の単語 $w_{m,n}\in\{1,\dots,V\}$
- その単語に紐づくトピック $z_{m,n}\in\{1,\dots,K\}$ で定まる、パラメタ $\beta_{z_{m,n}}$ のCategorical distributionに従う
$$ \begin{array} \ & p(w_{m,n}=v \mid z_{m,n}=k, \beta) = \beta_{k,v}\\ \text{where } &\sum_{v=1}^V \beta_{k,v} = 1~(k=1,\dots,K) \end{array} $$
生成モデル的な説明¶
- トピックごとの単語分布 $\beta_{k,v} = p(w_{m,n}=v \mid z_{m,n}=k)$ $(k=1,\dots,K, v=1,\dots,V)$ を決める
- トピックが $k$ だった時に単語 $v$ が出る確率
- $V$ 次元の多項分布が $K$ 個ある
- 文書 $m$ に対し、トピック分布のパラメタ $\theta_m\sim\mathrm{Dir}(\alpha)$ を決める
- $\theta_m\in\Delta^{K-1}$ は $K$ 次元ベクトルで、多項分布のパラメタ
- 文書 $m$ でのトピックの出やすさを決める
- 文書 $m$ の単語 $n$ のトピック $z_{m,n}\sim\mathrm{Multinomial}(\theta_m)$ を決める
- 文書 $m$ の単語 $n$ の単語 $w_{m,n}\sim\mathrm{Multinomial}(\beta_{z_{m,n}})$ を決める
グラフィカルモデル¶
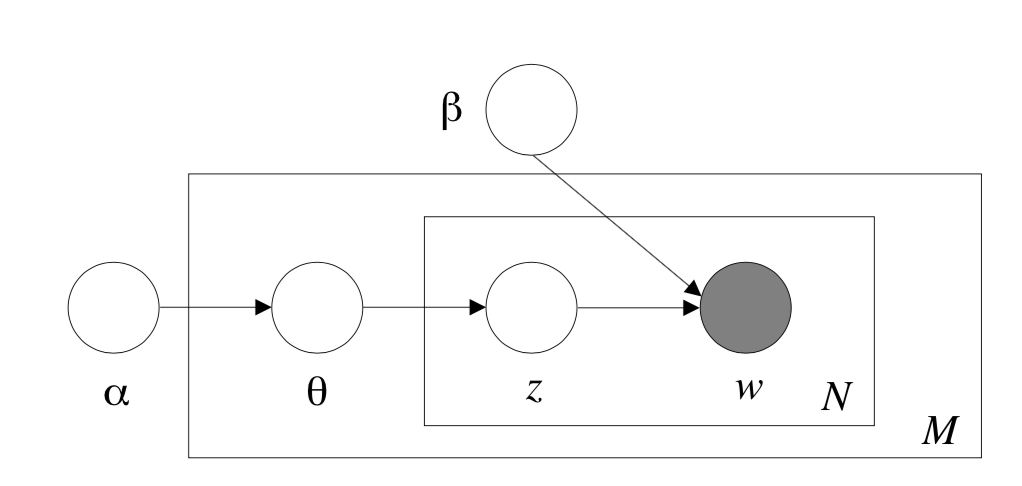
学習¶
データ $w=\{{w}_1,\dots,{w}_M\}$ が与えられた時、
- $\alpha$, $\beta_{k,v}~(k=1,\dots,K,\ v=1,\dots,V)$ をデータから推定する(最尤推定)
- $\alpha, \beta$ 固定の上で潜在変数 $\theta_{m}$, $z_{m,n}$ $(m=1,\dots,M,\ n=1,\dots,N_m)$ を推定する(inference)
Inference¶
- $(\alpha, \beta)$ は固定
- データ $w$ を与えた元での潜在変数 $(\theta, z)$ の事後分布を推定したい $$ p(\theta, z \mid w, \alpha, \beta) $$
事後分布は直接計算できない¶
$$ p(\theta, z \mid w, \alpha, \beta) = \dfrac{p(\theta, z, w \mid \alpha, \beta)}{p(w \mid \alpha, \beta)} $$
分子は計算できる $$ p(\theta, z, w \mid \alpha, \beta) = \prod_{m=1}^M \left[ p(\theta_m \mid \alpha) \prod_{n=1}^{N_m} \left[p(z_{m,n} \mid \theta_m) p(w_{m,n} \mid z_{m,n}, \beta)\right]\right] $$
分母は計算できない $$ \begin{align} p(w \mid \alpha, \beta) &=\prod_{m=1}^M \int \sum_{z} p(\theta_m, z_m, w_m \mid \alpha, \beta) \mathrm{d}\theta\\ &= \prod_{m=1}^M \dfrac{\Gamma(K\alpha)}{\Gamma(\alpha)^K} \int \left(\prod_{k=1}^K \theta_k^{\alpha-1}\right) \left( \prod_{n=1}^{N_m} \sum_{k=1}^K \prod_{v=1}^V (\theta_{m,k} \beta_{k,v})^{w_{m,n}} \right)\mathrm{d}\theta \end{align} $$
事後分布の変分近似¶
事後分布を以下の分布で近似する $$ \begin{align} q(\theta, z \mid \gamma, \phi) &= \prod_{m=1}^{M} q(\theta_m, z_m \mid \gamma_m, \phi_m)\\ q(\theta_m, z_m \mid \gamma_m, \phi_m)&=q(\theta_m \mid \gamma_m)\prod_{n=1}^{N_m}q(z_{m,n} \mid \phi_{m,n}) \end{align} $$
- $q(\theta_m \mid \gamma_m) = \mathrm{Dir}(\theta_m; \gamma_m)$
- $q(z_{m,n} \mid \phi_{m,n}) = \mathrm{Multinomial}(\phi_{m,n})$
事後分布の変分近似¶
- 元のモデル: $\theta_m$ と $z_m$ が従属
- 変分分布: $\theta_m$ と $z_m$ が独立
- 独立な場合は計算できることが多い
事後分布の変分近似¶
事後分布との距離が近くなるように $\gamma$ と $\phi$ を学習する
$$ (\gamma^\star, \phi^\star) = \arg\min_{\gamma, \phi} \mathrm{KL}(q(\theta, z \mid \gamma, \phi) || p(\theta, z \mid w, \alpha, \beta)) $$ ここで $q(\theta, z \mid \gamma, \phi) = \prod_{m=1}^M q(\theta_m, z_m \mid \gamma_m, \phi_m)$
事後分布の変分近似(文書 $m$ ごとに)¶
事後分布との距離が近くなるように $\gamma_m$ と $\phi_m$ を学習する
$$ (\gamma_m^\star, \phi_m^\star) = \arg\min_{\gamma_m, \phi_m} \mathrm{KL}(q(\theta_m, z_m \mid \gamma_m, \phi_m) || p(\theta_m, z_m \mid w_m, \alpha, \beta)) $$
補題1¶
以下の等式が成り立つ: $$ \mathrm{KL}(q(\theta_m, z_m \mid \gamma_m, \phi_m) || p(\theta_m, z_m \mid w_m, \alpha, \beta)) = \log p(w_m \mid \alpha, \beta) - \mathbb{E}_{q_m} \left[\log p(w_m, z_m, \theta_m \mid \alpha, \beta)\right] + \mathbb{E}_{q_m} \left[\log q(\theta_m, z_m \mid \gamma_m, \phi_m)\right] $$
左辺は事後分布 $p(\theta_m, z_m\mid w_m,\alpha, \beta)$があって計算できないが、右辺は事後分布がないため計算できることが嬉しい
証明¶
$$ \begin{align} \log p(w_m \mid \alpha, \beta) &= \log \int \sum_{z_m} p(w_m, \theta_m, z_m \mid \alpha, \beta) \mathrm{d}\theta_m\\ &=\log \int \sum_{z_m} \dfrac{p(w_m, \theta_m, z_m \mid \alpha, \beta)}{q(\theta_m, z_m \mid \gamma_m, \phi_m)} q(\theta_m, z_m \mid \gamma_m, \phi_m) \mathrm{d}\theta_m\\ &\geq \int \sum_{z_m} q(\theta_m, z_m \mid \gamma_m, \phi_m) \log \left( \dfrac{p(w_m, \theta_m, z_m \mid \alpha, \beta)}{q(\theta_m, z_m \mid \gamma_m, \phi_m)}\right) \mathrm{d}\theta_m \end{align} $$
証明¶
また $$ \begin{align} \log p(w_m \mid \alpha, \beta) = \int \sum_{z_m} q(\theta_m, z_m \mid \gamma_m, \phi_m) \log p(w_m \mid \alpha, \beta) \mathrm{d}\theta_m \end{align} $$ なので、(左辺) - (右辺)は、 $$ \begin{align} &\int \sum_{z_m} q(\theta_m, z_m \mid \gamma_m, \phi_m) \log \left( \dfrac{q(\theta_m, z_m \mid \gamma_m, \phi_m)p(w_m \mid \alpha, \beta)}{p(w_m, \theta_m, z_m \mid \alpha, \beta)}\right) \mathrm{d}\theta_m\\ =&\int \sum_{z_m} q(\theta_m, z_m \mid \gamma_m, \phi_m) \log \left( \dfrac{q(\theta_m, z_m \mid \gamma_m, \phi_m)}{p(\theta_m, z_m \mid w_m, \alpha, \beta)}\right) \mathrm{d}\theta_m\\ =& \mathrm{KL}(q(\theta_m, z_m \mid \gamma_m, \phi_m) || p(\theta_m, z_m \mid w_m, \alpha, \beta)) \end{align} $$
事後分布の変分近似(文書 $m$ ごとに)¶
事後分布との距離が近くなるように $\gamma_m$ と $\phi_m$ を学習する
$$ \begin{align} (\gamma_m^\star, \phi_m^\star) &= \arg\min_{\gamma_m, \phi_m} \mathrm{KL}(q(\theta_m, z_m \mid \gamma_m, \phi_m) || p(\theta_m, z_m \mid w_m, \alpha, \beta))\\ &= \arg\max_{\gamma_m, \phi_m}\left( \mathbb{E}_{q_m} \left[\log p(w_m, z_m, \theta_m \mid \alpha, \beta)\right] - \mathbb{E}_{q_m} \left[\log q(z_m, \theta_m \mid \gamma_m, \phi_m)\right]\right) \end{align} $$
目的関数を分解する¶
$$ \begin{align} &\mathbb{E}_{q_m} \left[\log p(w_m, z_m, \theta_m \mid \alpha, \beta)\right] - \mathbb{E}_{q_m} \left[\log q(z_m, \theta_m \mid \gamma_m, \phi_m)\right]\\ =& \mathbb{E}_{q_m} \left[\log p(\theta_m \mid \alpha)\right] + \mathbb{E}_{q_m} \left[\log p(z_m \mid \theta_m)\right] + \mathbb{E}_{q_m} \left[\log p(w_m \mid z_m, \beta)\right] \\ & - \mathbb{E}_{q_m} \left[\log q(\theta_m \mid \gamma_m)\right] - \mathbb{E}_{q_m} \left[\log q(z_m \mid \phi_m)\right] \end{align} $$
それぞれの項を計算してみる¶
第一項 $$ \begin{align} \mathbb{E}_{q_m} \left[\log p(\theta_m \mid \alpha)\right] &= \mathbb{E}_{q(\theta_m \mid \gamma_m)} \left[\log \Gamma\left(\sum_{k=1}^{K}\alpha_k\right) - \sum_{k=1}^K \log\Gamma(\alpha_k) + \sum_{k=1}^K (\alpha_k - 1) \log \theta_{m,k}\right]\\ &= \log \Gamma\left(\sum_{k=1}^{K}\alpha_k\right) - \sum_{k=1}^K \log\Gamma(\alpha_k) + \sum_{k=1}^K (\alpha_k - 1) \left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right) \end{align} $$
- $\Psi$ は digamma 関数(gamma関数を一階微分したもの)
- $\mathbb{E}_{q(\theta_m \mid \gamma_m)}[\log \theta_{m,k}]= \Psi\left(\alpha_k\right) - \Psi\left(\sum_{k=1}^K \alpha_k\right) $ を利用
参考¶
- Dirichlet 分布は指数分布族に属する
- 確率密度関数が $p(x \mid \eta) = h(x) \exp\left[\eta^\top T(x) - A(\eta)\right]$ とかけること
- $T(x) = \begin{bmatrix} \log \theta_1 & \dots & \log \theta_K \end{bmatrix}$
- $A(\eta) = \sum_{k=1}^K \log\Gamma(\alpha_k) -\log \Gamma\left(\sum_{k=1}^K \alpha_k \right)$
- 指数分布族では以下が成り立つことを利用 $$ \begin{align} \mathbb{E}_{p(x\mid \eta)}\left[T(x)\right] &= \int T(x) h(x) \exp(\eta^\top T(x)) \exp(-A(\eta)) \mathrm{d}x\\ &= \int \left(\dfrac{\partial}{\partial \eta} h(x) \exp(\eta^\top T(x))\right) \exp(-A(\eta)) \mathrm{d}x\\ &= \int \dfrac{\partial}{\partial \eta} \left(\left(h(x) \exp(\eta^\top T(x))\right) \exp(-A(\eta))\right) - \left(h(x) \exp(\eta^\top T(x))\right) \dfrac{\partial}{\partial \eta}\exp(-A(\eta))\mathrm{d}x\\ &= 0 - \int \left(h(x) \exp(\eta^\top T(x))\right) \dfrac{\partial}{\partial \eta}\exp(-A(\eta))\mathrm{d}x = \dfrac{\partial}{\partial \eta}A(\eta) \end{align} $$
それぞれの項を計算してみる¶
第二項 $$ \begin{align} \mathbb{E}_{q_m} \left[\log p(z_m \mid \theta_m)\right] &= \mathbb{E}_{q_m}\left[\sum_{n=1}^{N_m} \log p(z_{m,n} \mid \theta_m)\right]\\ &= \mathbb{E}_{q(\theta_m \mid \gamma_m)}\left[ \sum_{n=1}^{N_m} \sum_{k=1}^K q(z_{m,n}=k \mid \phi_{m,n}) \log p(z_{m,n}=k \mid \theta_m)\right]\\ &=\mathbb{E}_{q(\theta_m \mid \gamma_m)}\left[ \sum_{n=1}^{N_m} \sum_{k=1}^K \phi_{m,n,k} \log \theta_{m,k}\right]\\ &=\sum_{n=1}^{N_m} \sum_{k=1}^K \phi_{m,n,k} \left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right) \end{align} $$
それぞれの項を計算してみる¶
第三項 $$ \begin{align} \mathbb{E}_{q_m} \left[\log p(w_m \mid z_m, \beta)\right] &= \sum_{n=1}^{N_m} \mathbb{E}_{q(z_{m,n} \mid \phi_{m,n})} \left[\log p(w_{m,n} \mid z_{m,n}, \beta)\right] \\ &= \sum_{n=1}^{N_m} \sum_{k=1}^K \phi_{m,n,k} \log p(w_{m,n} \mid z_{m,n}=k, \beta)\\ &= \sum_{n=1}^{N_m} \sum_{k=1}^K \sum_{v=1}^{V} \phi_{m,n,k} \mathbb{1}[w_{m,n} = v] \log \beta_{k, v} \end{align} $$
それぞれの項を計算してみる¶
第四項 $$ \begin{align} \mathbb{E}_{q_m} \left[\log q(\theta_m \mid \gamma_m)\right] &= \mathbb{E}_{q(\theta_m \mid \gamma_m)} \left[\log \Gamma\left(\sum_{k=1}^{K}\gamma_{m,k}\right) - \sum_{k=1}^K \log \Gamma(\gamma_{m,k}) + \sum_{k=1}^K (\gamma_{m,k} - 1) \log \theta_{m,k}\right]\\ &= \log \Gamma\left(\sum_{k=1}^{K}\gamma_{m,k}\right) - \sum_{k=1}^K \log \Gamma(\gamma_{m,k}) + \sum_{k=1}^K (\gamma_{m,k} - 1) \left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right) \end{align} $$
それぞれの項を計算してみる¶
第五項 $$ \begin{align} \mathbb{E}_{q_m} \left[\log q(z_m \mid \phi_m)\right] &= \sum_{n=1}^{N_m} \mathbb{E}_{q(z_{m,n} \mid \phi_{m,n})} \left[\log q(z_{m,n} \mid \phi_{m,n})\right] \\ &=\sum_{n=1}^{N_m} \sum_{k=1}^K \phi_{m,n,k} \log \phi_{m,n,k} \end{align} $$
まとめると(文書$m$に関する)目的関数は...¶
$$ \begin{align} &L_m(\gamma, \phi; \alpha, \beta) \\ =& \log \Gamma\left(\sum_{k=1}^{K}\alpha_k\right) - \sum_{k=1}^K \log\Gamma(\alpha_k) + \sum_{k=1}^K (\alpha_k - 1) \left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right) \\ &+ \sum_{n=1}^{N_m} \sum_{k=1}^K \phi_{m,n,k} \left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right) \\ &+ \sum_{n=1}^{N_m} \sum_{k=1}^K \sum_{v=1}^{V} \phi_{m,n,k} \mathbb{1}[w_{m,n} = v] \log \beta_{k, v}\\ &- \left( \log \Gamma\left(\sum_{k=1}^{K}\gamma_{m,k}\right) - \sum_{k=1}^K \log\Gamma(\gamma_{m,k}) + \sum_{k=1}^K (\gamma_{m,k} - 1) \left( \Psi(\gamma_k) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right)\right)\\ &- \sum_{n=1}^{N_m} \sum_{k=1}^K \phi_{m,n,k} \log \phi_{m,n,k} \end{align} $$
$\phi$ に関する最大化($\gamma$ は固定)¶
各 $m,n$ について $\sum_{k=1}^K \phi_{m,n,k} = 1$ のもとで最大化
ラグランジアンは
$$ \begin{align} \ &L_m(\phi) \\ =&\sum_{n=1}^{N_m} \sum_{k=1}^K \phi_{m,n,k} \left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right) \\ +& \sum_{n=1}^{N_m} \sum_{k=1}^K \sum_{v=1}^{V} \phi_{m,n,k} \mathbb{1}[w_{m,n} = v] \log \beta_{k, v}\\ -& \sum_{n=1}^{N_m} \sum_{k=1}^K \phi_{m,n,k} \log \phi_{m,n,k}\\ +& \sum_{n=1}^{N_m}\lambda_n \left(\sum_{k=1}^K \phi_{m,n,k}-1\right) \end{align} $$
$\phi$ に関する最大化($\gamma$ は固定)¶
$\phi_{m,n,k}$ で微分すると
$$ \begin{align} \ &\dfrac{\partial}{\partial \phi_{m,n,k}}L_m(\phi) \\ = &\Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) + \sum_{v=1}^{V} \mathbb{1}[w_{m,n} = v] \log \beta_{k, v}- \log \phi_{m,n,k} - 1 + \lambda_n=0 \end{align} $$
$\phi$ に関する最大化($\gamma$ は固定)¶
整理すると
$$ \begin{align} \phi_{m,n,k} \propto \exp\left[\Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) + \sum_{v=1}^{V} \mathbb{1}[w_{m,n} = v] \log \beta_{k, v} \right] \end{align} $$
$\lambda_n$ は正規化に使われる
$\gamma$ に関する最大化($\phi$ は固定)¶
$\gamma_{m,k}$ に関する項は
$$ \begin{align} &L_m(\gamma) \\ =& \sum_{k=1}^K (\alpha_k - 1) \left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right) \\ &+ \sum_{n=1}^{N_m} \sum_{k=1}^K \phi_{m,n,k} \left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right) \\ &- \left( \log \Gamma\left(\sum_{k=1}^{K}\gamma_{m,k}\right) - \sum_{k=1}^K\log\Gamma(\gamma_{m,k}) + \sum_{k=1}^K (\gamma_{m,k} - 1) \left( \Psi(\gamma_k) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right)\right) \end{align} $$
$\gamma$ に関する最大化($\phi$ は固定)¶
整理すると
$$ \begin{align} &L_m(\gamma) \\ =& \sum_{k=1}^K \left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k^\prime=1}^K \gamma_{m,k^\prime}\right) \right) \left(\alpha_k - \gamma_{m,k} + \sum_{n=1}^{N_m} \phi_{m,n,k}\right) \\ &- \left( \log \Gamma\left(\sum_{k=1}^{K}\gamma_{m,k}\right) - \sum_{k=1}^K \log\Gamma(\gamma_{m,k}) \right) \end{align} $$
$\gamma$ に関する最大化($\phi$ は固定)¶
$\gamma_{m,k}$ で微分すると
$$ \begin{align} &\dfrac{\partial}{\partial \gamma_{m,k}}L_m(\gamma) \\ = &- \Psi(\gamma_{m,k}) + \Psi\left(\sum_{k^\prime=1}^K \gamma_{m,k^\prime}\right)\\ &+ \Psi^\prime(\gamma_{m,k}) \left(\alpha_k - \gamma_{m,k} + \sum_{n=1}^{N_m} \phi_{m,n,k}\right) \\ &- \Psi^\prime\left(\sum_{k^\prime=1}^K \gamma_{m,k^\prime}\right)\sum_{k=1}^K \left(\alpha_k - \gamma_{m,k} + \sum_{n=1}^{N_m} \phi_{m,n,k}\right) \\ &- \Psi\left(\sum_{k^\prime=1}^K \gamma_{m,k^\prime}\right) + \Psi(\gamma_{m,k})\\ =& \Psi^\prime(\gamma_{m,k}) \left(\alpha_k - \gamma_{m,k} + \sum_{n=1}^{N_m} \phi_{m,n,k}\right) \\ &- \Psi^\prime\left(\sum_{k^\prime=1}^K \gamma_{m,k^\prime}\right)\sum_{k=1}^K \left(\alpha_k - \gamma_{m,k} + \sum_{n=1}^{N_m} \phi_{m,n,k}\right) \\ \end{align} $$
$\gamma$ に関する最大化($\phi$ は固定)¶
$\Psi^\prime$ の中身は忘れて係数を見ると、以下の$\gamma$で勾配が0になる
$$ \begin{align} \gamma_{m,k} = \alpha_k + \sum_{n=1}^{N_m} \phi_{m,n,k} \end{align} $$
Inference アルゴリズム¶
- $\phi_{m,n,k}$, $\gamma_{m,k}$ を初期化 $(m=1,\dots,M,\ n=1,\dots,N_{m},\ k=1,\dots,K)$.
- 以下を収束するまで繰り返す
- $$\begin{align} \phi_{m,n,k} \propto \exp\left[\Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) + \sum_{v=1}^{V} \mathbb{1}[w_{m,n} = v] \log \beta_{k, v} \right] \end{align} $$
- $$ \begin{align} \gamma_{m,k} = \alpha_k + \sum_{n=1}^{N_m} \phi_{m,n,k} \end{align} $$
$\alpha$, $\beta_{k,v}~(k=1,\dots,K,\ v=1,\dots,V)$ をデータから推定¶
- 上の Inference アルゴリズムを使うと、対数尤度の最もタイトな下界が求まる
- 下の式の右辺を $\phi, \gamma$ について最大化していた
- 対数尤度の下界を $\alpha, \beta$ について最大化すれば尤度を大きくできそう? $$ \begin{align} \log p(w_m \mid \alpha, \beta) \geq \int \sum_{z_m} q(\theta_m, z_m \mid \gamma_m, \phi_m) \log \left( \dfrac{p(w_m, \theta_m, z_m \mid \alpha, \beta)}{q(\theta_m, z_m \mid \gamma_m, \phi_m)}\right) \mathrm{d}\theta_m \end{align} $$
$\beta$ に関する最大化¶
下界の $\beta$ に関する項 + ラグランジアンは、 $$ \begin{align} L(\beta) = \sum_{m=1}^M \sum_{n=1}^{N_m} \sum_{k=1}^K \sum_{v=1}^{V} \phi_{m,n,k} \mathbb{1}[w_{m,n} = v] \log \beta_{k, v} + \sum_{k=1}^K \lambda_k \left(\sum_{v=1}^V \beta_{k,v} - 1\right) \end{align} $$
$\beta$ に関する最大化¶
$\beta_{k,v}$で微分すると $$ \begin{align} \dfrac{\partial}{\partial \beta_{k,v}}L(\beta) = \sum_{m=1}^M \sum_{n=1}^{N_m} \dfrac{1}{\beta_{k,v}}\phi_{m,n,k} \mathbb{1}[w_{m,n} = v] + \lambda_k \end{align} $$
$\beta$ に関する最大化¶
$\beta_{k,v}$で微分すると $$ \begin{align} \beta_{k,v} \propto \sum_{m=1}^M \sum_{n=1}^{N_m} \phi_{m,n,k} \mathbb{1}[w_{m,n}=v] \end{align} $$
$\alpha$ に関する最大化¶
下界の$\alpha$に関する項は、
$$ \begin{align} &L(\alpha) \\ =& \sum_{m=1}^M \left[\log \Gamma\left(\sum_{k=1}^{K}\alpha_k\right) - \sum_{k=1}^K \log\Gamma(\alpha_k) + \sum_{k=1}^K (\alpha_k - 1) \left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right)\right] \end{align} $$
$\alpha$ に関する最大化¶
下界の$\alpha_k$に関する勾配は、
$$ \begin{align} &\dfrac{\partial}{\partial\alpha_k}L(\alpha) \\ =& M \left(\Psi\left(\sum_{k=1}^{K}\alpha_k\right) - \Psi(\alpha_k) \right) + \sum_{m=1}^M\left( \Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) \right) \end{align} $$
$\alpha$ に関する最大化¶
勾配=0は解けないので、勾配法で最大化する
$\alpha, \beta$ の推定アルゴリズム¶
- $\alpha_k$ $(k=1,\dots,K)$, $\beta_{k,v}$ $(k=1,\dots,K,\ v=1,\dots,V)$ を初期化
- $\phi_{m,n,k}$, $\gamma_{m,k}$ を初期化 $(m=1,\dots,M,\ n=1,\dots,N_{m},\ k=1,\dots,K)$.
- 以下を収束するまで繰り返す
- 変分下界の更新(E-step) $$\begin{align} \phi_{m,n,k} &\propto \exp\left[\Psi(\gamma_{m,k}) - \Psi\left(\sum_{k=1}^K \gamma_{m,k}\right) + \sum_{v=1}^{V} \mathbb{1}[w_{m,n} = v] \log \beta_{k, v} \right]\\ \gamma_{m,k} &= \alpha_k + \sum_{n=1}^{N_m} \phi_{m,n,k} \end{align} $$
- $\beta$ の更新(M-step 1) $$ \begin{align} \beta_{k,v} &\propto \sum_{m=1}^M \sum_{n=1}^{N_m} \phi_{m,n,k} \mathbb{1}[w_{m,n}=v]\\ \end{align} $$
- $\alpha$ の更新(M-step 2) $$ \begin{align} \alpha_k &\leftarrow \alpha_k + \eta \dfrac{\partial}{\partial \alpha_k} L(\alpha) \end{align} $$ を収束するまで繰り返す。