応用計量分析２（第4回）

線形代数

担当教員: 梶野 洸（かじの ひろし）

本日の目標

• 線形代数を思い出す
• Python で線形代数の数値計算をやる
• 主成分分析（PCA）を実装する

線形代数で使うオブジェクト

• ベクトル $x = \begin{bmatrix} 1 \\ 0 \end{bmatrix}$

import numpy as np # 
x = np.array([1.0, 0.0])
print(x)

[1. 0.]

なぜ numpy を使うか？

• それぞれリストでも書けるがリストだと演算が定義されていない。
  • ベクトルの足し算
  • 行列の掛け算など
• numpy では array の間の演算として定義されている。

ベクトル

$x=\begin{bmatrix}1 \\ 0 \end{bmatrix}$, $y=\begin{bmatrix}0 \\ 1\end{bmatrix}$ とする

x = np.array([1.0, 0])
y = np.array([0, 1.0])
print(x, y)

[1. 0.] [0. 1.]

• ベクトルのスカラー倍: $3x$

print(3 * x)

[3. 0.]

• ベクトル同士の足し算・引き算: $x + y$, $x - y$
• より一般的に線形結合: $3x - 10y$

print(x + y)
print(x - y)
print(3 * x - 10 * y)

[1. 1.]
[ 1. -1.]
[  3. -10.]

• 内積: $x \cdot y$, $(3x - y) \cdot (x+2y)$

print(x @ y)
print((3 * x - y) @ (x + 2 * y))

print(np.dot(x, y)) # 関数の形で書くこともできる

0.0
1.0
0.0

※内積は、2つベクトルを受け取って、1つのスカラーを返す関数としても書ける

• ノルム: $\|2x - y\|_2$

print(((2 * x - y) @ (2 * x - y)) ** (0.5)) # 内積を使って計算した場合
print(np.linalg.norm(2 * x - y)) # numpyの関数を使って計算した場合

2.23606797749979
2.23606797749979

• 要素積（アダマール積）: $x\circ y$

各次元で積を取る演算

print(x * y)

[0. 0.]

ここまでのまとめ

• ベクトルはnumpyの array というオブジェクトで定義する
• 普通の数値と同じような演算ができる
• 内積やノルムなど、線形代数特有の計算は関数を用いて計算する
  • 内積: np.dot
  • ノルム: np.linalg.norm

想定QA

Q. 欲しい関数があるかどうか調べたい

A. ググるかライブラリのAPIを見る（numpyはここ）

Q. np.dot とか np.linalg.norm とかなんやねん

A. ライブラリは階層構造になっている。

• np.dot は、numpy (npと書いてる)直下に定義された dot という関数、
• np.linalg.norm は、numpy の下の linalg (linear algebra; 線形代数)という線形代数の関数をまとめた集まりのなかの norm という関数 と解釈する

Q. じゃあ np.array は？

A. オブジェクトを作る関数と言ってもいいかも。

リストを受け取って array を返す

行列

$A = \begin{bmatrix} 1 & 1 \\ 0 & 2 \end{bmatrix}$

# np.array にリストのリストを渡すと行列
A = np.array([[1.0, 1.0], [0.0, 2.0]])
print(A)

[[1. 1.]
 [0. 2.]]

行列とベクトルの積

$Ax$

$x^\top A$

print(A @ x)
print(x @ A)

[1. 0.]
[1. 1.]

print(A @ np.array([1,2,3,4])) # 2x2の行列に4次元のベクトルは掛けられない

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-22-a386da54a8ef> in <module>()
----> 1 print(A @ np.array([1,2,3,4])) # 2x2の行列に4次元のベクトルは掛けられない

ValueError: shapes (2,2) and (4,) not aligned: 2 (dim 1) != 4 (dim 0)

行列と行列の積

$A = \begin{bmatrix} 1 & 1 \\ 0 & 2 \end{bmatrix}$, $B = \begin{bmatrix} 0 & 1 \\ 1 & 2 \end{bmatrix}$

A = np.array([[1.0, 1.0],
              [0.0, 2.0]])
B = np.array([[0.0, 1.0],
              [1.0, 2.0]])
print(A @ B)
print(B @ A)

[[1. 3.]
 [2. 4.]]
[[0. 2.]
 [1. 5.]]

演習

• $A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}$ の絶対値が最大の固有値とそれに対応する固有ベクトルを計算せよ

指針

1. 手計算
2. numpy で実装されているのをつかう
3. べき乗法

np.linalg.eigvals(np.array([[2,1],[1,2]]))

array([3., 1.])

手計算

• 固有値、固有ベクトルの定義: $A v = \lambda v$ を満たす $\lambda$, $v (\neq 0)$
• 線形方程式 $(A - \lambda I)v = 0$ が非自明な解（つまり$v\neq 0$）を持つような $\lambda$ を見つければよい
• 特性方程式 $\mathrm{det}(A-\lambda I)=0$ の解が固有値
• $\mathrm{det}(A-\lambda I) = (2-\lambda)(2-\lambda)-1 \\= \lambda^2 - 4\lambda + 3 = (\lambda-3)(\lambda - 1)=0$
• 絶対値が最大の固有値は $3$
• $(A - \lambda I)v = \begin{bmatrix} -1 & 1\\1 & -1 \end{bmatrix}\begin{bmatrix}v_1\\ v_2 \end{bmatrix}=0$
• $v_1 = v_2$ を満たせばよいので、例えば $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$ が固有ベクトル。

numpy で実装されているのを使う

A = np.array([[2, 1], [1, 2]])
np.linalg.eig(A)

(array([3., 1.]), array([[ 0.70710678, -0.70710678],
        [ 0.70710678,  0.70710678]]))

絶対値最大の固有値は $3$、対応する固有ベクトルは $\begin{bmatrix}0.70710678\\ 0.70710678 \end{bmatrix}$

（返り値の解釈は、APIを見ましょう）

べき乗法

• $A\in\mathbb{R}^{N\times N}$ の固有値と対応する固有ベクトルを $\lambda_1,\dots,\lambda_N$, $v_1,\dots,v_N$ とする。
• $|\lambda_1| > |\lambda_2| > \cdots > |\lambda_N|$ とする。

任意のベクトル $x\in\mathbb{R}^N$ は、固有ベクトルで展開できる（固有ベクトルは基底を成す）:

$\begin{eqnarray} x = \sum_{n=1}^{N}c_n v_n \end{eqnarray}$

$A$ を掛け続けると絶対値最大の固有値に対応する固有ベクトルが（相対的に）強調される:

$\begin{eqnarray} A^k x &= \sum_{n=1}^{N}c_n A^k v_n = \sum_{n=1}^N c_n \lambda_n^k v_n\\ &= \lambda_1^k \sum_{n=1}^N c_n \left(\frac{\lambda_n}{\lambda_1}\right)^k v_n\\ &\approx \lambda_1^k c_1 v_1 \end{eqnarray}$

• 適当なベクトルに行列 $A$ を掛け続けると $v_1$ が求まる
• $\lambda_1 = \dfrac{v_1^\top A v_1}{v_1^\top v_1}$

A = np.array([[2, 1], [1, 2]])
x = np.array([1, 2])
for _ in range(100):
    x = A @ x
    x = x / np.linalg.norm(x) # ベクトルを正規化しないと数値誤差が乗る
print(x@A@x / (x@x), x)

3.0 [0.70710678 0.70710678]

線形方程式

$A\in\mathbb{R}^{N\times N}$, $b\in\mathbb{R}^N$ としたとき、 $Ax=b$ を満たす $x\in\mathbb{R}^N$ を求める。

$A$ が正則行列（＝逆行列を持つ）のとき、 $x = A^{-1}b$ が解。

二通りの実装方法がある

• 逆行列を求めるアルゴリズム(Gauss-Jordanなど)を利用
• 直接線形方程式を解くアルゴリズム(LU分解)を利用

！！なるべく直接線形方程式を解くアルゴリズムを利用すべき！！

• LU 分解の方がそもそも速い
  • $A$ の形によっては更に速くなる
• numpy では逆行列を求めるのに$AX=I$を解いている（＝線形方程式を解くのと同じ計算時間がここで必要）
  • さらに $A^{-1}b$ を計算しないといけないので計算時間的に損

（参考）伊理正夫, 藤野和建: 数値計算の常識

ここまでのまとめ

• ベクトル、行列は numpy を使う
• 固有値・固有ベクトルなどの計算もできる
• 線形方程式も解ける
• 逆行列を求める必要があるか考える（線形方程式を解けばいい場合は線形方程式を解く）

主成分分析, PCA

データ $x_1,\dots,x_N\in \mathbb{R}^D$ があったとき、その"特性"を保ったまま低次元表現を得たい。

• データを目で見たい（100次元だと見られないけど2次元なら）
• 同じ情報量ならば低次元の方が学習しやすい
• 特性の定義によって様々な手法がある
• $K~(<D)$次元表現を得る

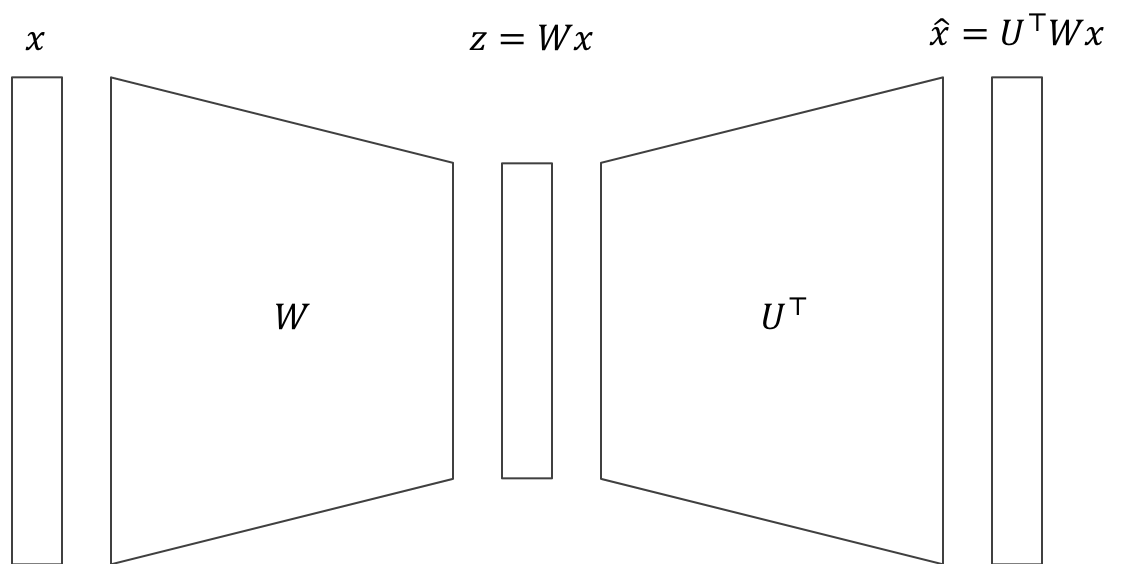
PCA は、次のような線形変換のペア $W, U$ を求めるという気持ち:

• 入力 $x\in\mathbb{R}^D$
• 低次元表現 $z = Wx$ ($W\in\mathbb{R}^{K\times D}$)
• 低次元表現から入力を復元 $\hat{x} = U^\top z = U^\top W x$ ($U\in\mathbb{R}^{K\times D}$)
• $\hat{x}\approx x$ となってほしい

定式化

• $X = \begin{bmatrix} x_1 & x_2 & \dots & x_N \end{bmatrix}^\top$
• 平均$0$であるとする: $\sum_{n=1}^N x_n = 0$
• 以下を満たす $W, U$ を求める

$$ \min_{W, U\in\mathbb{R}^{K\times D}} \sum_{n=1}^{N}\|x_n - U^{\top}Wx_n\|_{2}^2 \tag{1} $$

補題1

式(1)の最適値は

$$ \begin{align} \min_{V\in\mathbb{R}^{K\times D},\ VV^\top=I} \sum_{n=1}^{N}\|x_n - V^{\top}Vx_n\|_{2}^2\tag{2} \end{align} $$

の最適値と等しい

証明

• $R = \{U^\top W x \mid x \in \mathbb{R}^D\}$ とすると、$R$は$\mathbb{R}^D$中の$K$次元線型部分空間
• $R$ の正規直交基底を$V=\begin{bmatrix}v_1 & \dots & v_K\end{bmatrix}^\top\in\mathbb{R}^{D\times K}$とする。
• $V^\top Vx = \arg\min_{\tilde{x}\in R} \|x - \tilde{x}\|$が成り立つ。
  • $R$ の元は $y\in\mathbb{R}^K$ を用いて $V^\top y$ と書けることを利用して示す（演習）
• 式(1)の最適解 $U^\star$, $W^\star$ と、それに対応する $R^\star$, $V^\star$ を持ってくると、 $$ \begin{align} \|x_n - {U^\star}^\top W^\star x_n\|^2 \geq \min_{\tilde{x}_n\in R^\star}\|x_n - \tilde{x}_n\|^2 = \|x_n - {V^\star}^\top V^\star x_n\|^2 \end{align} $$
• $U^\star, W^\star$ も $V^\star$ も最適解なので、上式は等号成立。

補題2

最適化問題(2)は $$ \max_{V\in\mathbb{R}^{K\times D}, VV^\top=I}\mathrm{tr}\left(V \left(\sum_{n=1}^N x_n x_n^\top\right)V^\top\right) \tag{3} $$ と同値。

証明

展開すれば良い。

$$ \sum_{n=1}^N \|x_n - V^\top V x_n\|^2 = \sum_{n=1}^N \|x_n\|^2 - 2\sum_{n=1}^N x_n^\top V^\top V X_n + \sum_{n=1}^N x_n^\top V^\top V V^\top V x_n $$

$$ =\sum_{n=1}^N \|x_n\|^2 - \sum_{n=1}^N x_n^\top V^\top V x_n $$

第二項は、

$$ \begin{align} \sum_{n=1}^N x_n^\top V^\top V x_n = \sum_{n=1}^N \mathrm{tr}(x_n^\top V^\top V x_n) = \sum_{n=1}^N \mathrm{tr}(x_n x_n^\top V^\top V) \\ = \mathrm{tr}\left(\left(\sum_{n=1}^N x_n x_n^\top\right) V^\top V\right) = \mathrm{tr}\left(V\left(\sum_{n=1}^N x_n x_n^\top\right) V^\top\right) \end{align} $$

補題3

$A=\sum_{n=1}^N x_n x_n^\top$ として、その固有値、固有ベクトルを $\lambda_1,\dots, \lambda_D$, $u_1,\dots,u_D$ とする（$\lambda_1\geq\lambda_2\geq\cdots\geq\lambda_D$）。 この時任意の $V\in\mathbb{R}^{K\times D}, VV^\top=I$ について

$$ \mathrm{tr}\left(V A V^\top\right) \leq \max_{w\in[0,1]^D, \sum_{d=1}^D w_d\leq K}\sum_{d=1}^D \lambda_d w_d = \sum_{d=1}^K \lambda_d $$

が成立

証明

$A=U^\top \Lambda U$ と固有値分解できる（$U\in\mathbb{R}^{D\times D}$）。 $V\in\mathbb{R}^{K\times D}, VV^\top = I$ を一つ持ってくる。

$W=VU^\top\in\mathbb{R}^{K\times D}$と置くと、

• $VAV^\top = VU^\top\Lambda U V^\top = W\Lambda W^\top$.
• $W$ の各行は$D$次元空間の正規直交基底: $WW^\top = UV^\top VU^\top = I$

$$ \begin{align} \mathrm{tr}(W\Lambda W^\top) = \sum_{d=1}^D \lambda_d \sum_{k=1}^Kw_{k,d}^2 \end{align} $$

$w_d:=\sum_{k=1}^K w_{k,d}^2$ と置くと、

$$ \begin{align} \mathrm{tr}(W\Lambda W^\top) &= \sum_{d=1}^D \lambda_d \sum_{k=1}^Kw_{k,d}^2\\ &= \sum_{d=1}^D \lambda_d w_d \end{align} $$

ここで $0\leq\sum_{k=1}^K w_{k,d}^2 \leq 1~(d=1,\dots,D)$, $\sum_{d=1}^D \sum_{k=1}^K w_{k,d}^2=K$ なので、

$$ \begin{align} \mathrm{tr}(W\Lambda W^\top) &= \sum_{d=1}^D \lambda_d w_d\\ &\leq \max_{w_d\in[0,1], \sum_{d=1}^D w_d\leq K}\sum_{d=1}^D \lambda_d w_d \end{align} $$ が成立.

定理

$A=\sum_{n=1}^N x_n x_n^\top$ として、その固有値、固有ベクトルを $\lambda_1,\dots, \lambda_D$, $u_1,\dots,u_D$ とする（$\lambda_1\geq\lambda_2\geq\cdots\geq\lambda_D$）。

この時 $V = \begin{bmatrix}u_1 \dots u_K\end{bmatrix}^\top$ が最適化問題(2), (3)の解

証明

$$ \mathrm{tr}(VAV^\top) = \mathrm{tr}(VU^\top \Lambda UV^\top) = \mathrm{tr}(\mathbb{1}_K \Lambda \mathbb{1}_K) = \sum_{d=1}^K \lambda_d $$ が成り立つ。ここで $$ [\mathbb{1}_K]_{i,j} = \begin{cases} \delta_{i,j} &\text{ if } i=j\leq K\\ 0 & \text{otherwise}. \end{cases} $$

補題3より、これは最適値。

アルゴリズム

• 入力: $x_1,\dots, x_N\in\mathbb{R}^D$, $K\in\mathbb{N}$
• 出力: $z_1,\dots, z_N\in\mathbb{R}^K$

1. $A=\sum_{n=1}^N x_n x_n^\top$
2. $A$ の固有値と対応する固有ベクトル $(\lambda_1, u_1),\dots,(\lambda_D, u_D)$ を求める（$\lambda_1\geq\cdots\geq \lambda_D$）
3. $V=\begin{bmatrix}u_1 \dots u_K\end{bmatrix}^\top$ として、$z_n=Vx_n$ を計算

ここまでのまとめ

• PCA はデータを低次元空間に落とす方法
• 再構成時の損失を最小化するようにする

PCA の実装

• PCA でデータを2次元で見てみる
• 主成分を見てみる
• 再構成してみる

import matplotlib.pyplot as plt
from sklearn.datasets import fetch_olivetti_faces

# データを取得
dataset = fetch_olivetti_faces()
num_examples, row_size, col_size = dataset['images'].shape
X = dataset['data']

# 平均0にしておく（しなくてもまあ大丈夫だけど）
X_mean = X.mean(axis=0)
X_centered = X - X_mean

# 顔データを表示してみる
plt.imshow(dataset['images'][0], cmap=plt.cm.gray)
plt.show()
X.shape

(400, 4096)

演習

PCA を実行する関数を書け

• 入力: データ $X\in\mathbb{R}^{N\times D}$, 次元 $K$
• 出力: 変換されたデータ $Z\in\mathbb{R}^{N\times K}$, 変換にもちいる線形変換 $V\in\mathbb{R}^{D\times K}$

ヒント: 対称行列の固有値分解を行う関数 https://docs.scipy.org/doc/scipy/reference/generated/scipy.linalg.eigh.html#scipy.linalg.eigh

from scipy.linalg import eigh
def pca(X, K):
    A = X.T @ X
    eig_val, eig_vec = eigh(A)
    V = eig_vec[:, -K:]
    z = X @ V
    return z, V

# pca を実行
K=20
z, V = pca(X_centered, K)

# V の行ベクトルが正規直交基底であることを確認
print('distance from the identity:', np.abs(V.T @ V - np.identity(K)).max())

print('mean reconstruction loss: ',((X_centered - z @ V.T) * (X_centered - z @ V.T)).mean())

distance from the identity: 1.5404075384140015e-06
mean reconstruction loss:  0.0045594834

# データの貼る空間の固有ベクトルを見てみる
plt.imshow(-V[:, -1].reshape(row_size, col_size), cmap=plt.cm.gray)
plt.show()

plt.scatter(z[:, 0], z[:, 1])

<matplotlib.collections.PathCollection at 0x1a202855f8>

# この場合は2次元に落としてもよくわからない...
import matplotlib.cm as cm
import numpy as np

colors = cm.rainbow(np.linspace(0, 1, 10))
for each_idx in range(100):
    plt.scatter(z[each_idx, 0], z[each_idx, 1], color=colors[dataset['target'][each_idx]])
plt.show()

# 再構成
X_rec = z @ V.T + X_mean
idx = 190

f, (ax1, ax2) = plt.subplots(1, 2)
ax1.imshow(dataset['images'][idx], cmap=plt.cm.gray) # 左が元の画像
ax2.imshow(X_rec[idx].reshape(row_size, col_size), cmap=plt.cm.gray) # 右が再構成画像
plt.show()

まとめ

• 行列、ベクトルは numpy を使って実装する
• 線形代数の操作は numpy の API を探せば実装されていることが多い
• 主成分分析(principle component analysis; PCA) を実装した
  • データを低次元空間に射影するアルゴリズム
  • 再構成時の損失を最小化する
  • 固有値分解に帰着される