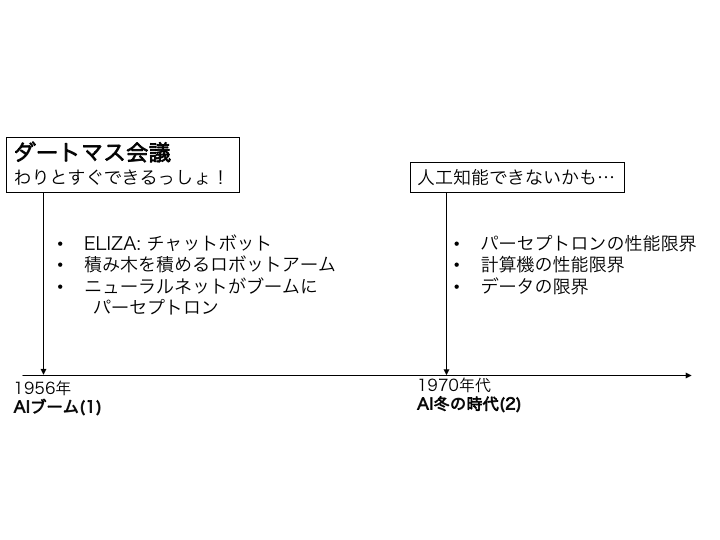
人工知能の歴史 (2/3)¶
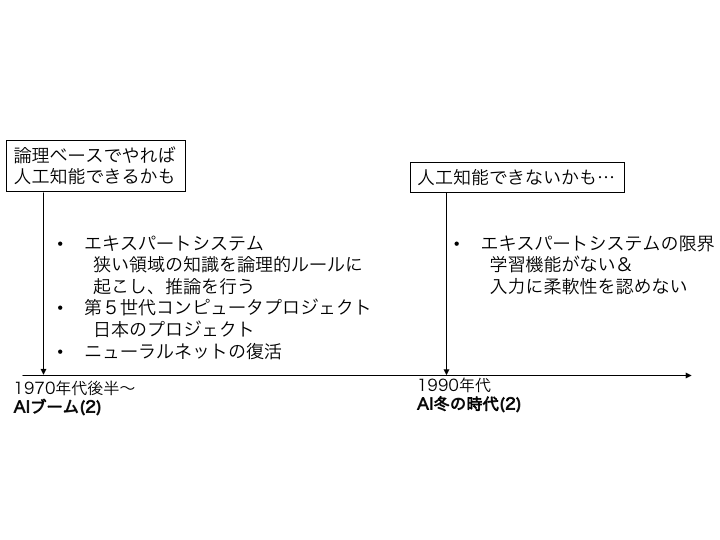
人工知能の歴史 (3/3)¶
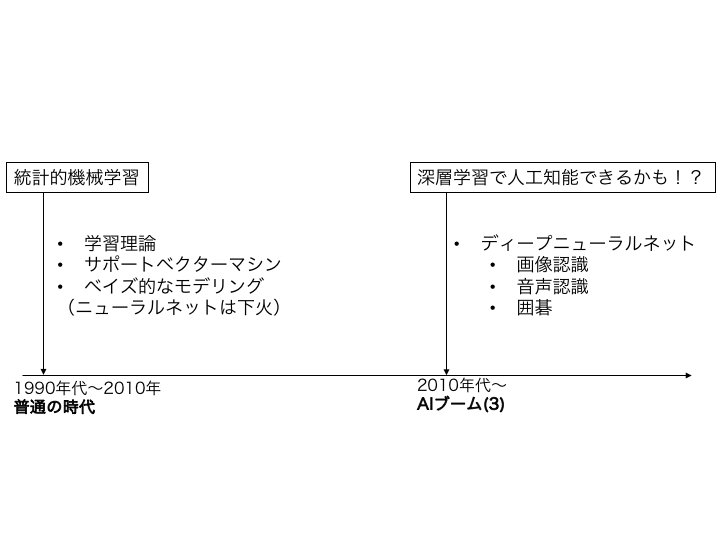
人工知能の歴史(まとめ)¶
- 人工知能は何度もブームになっては冬の時代を迎えている
- ニューラルネットは何度も死んでは生き返っている
- 論理を用いたもの、統計を用いたものなど、様々な流派がある
- それぞれ利点・欠点がある
- それぞれ単体では人工知能は実現できないのかも?
- この授業では統計的機械学習を取り扱います
統計的機械学習の枠組み¶
データが従う規則(=確率分布、関数)を有限個のデータから推定する問題
- サンプル: $\mathcal{D} = \{z_n\in\mathcal{Z} \mid n=1,\dots,N\}$
- 仮定: $z_n \overset{\mathrm{iid}}{\sim} p^\star(Z)$ ($p^\star$: 未知の確率分布)
- パラメトリックモデル $\mathcal{M}=\{p(Z ; \theta) \mid \theta\in\Theta\}$ の中から $p^\star$ に近いものをサンプルから推定する
例1: 画像認識¶
画像に猫がいるかいないか判別する規則をデータから推定したい
- $z_n=(x_n, y_n)$:
- $x_n\in\mathbb{R}^{H\times W\times C}$ は画像
- $y_n\in\{0,1\}$ はラベル(0=猫がいない, 1=猫がいる)
- $p(y\mid x)$ を推定したい
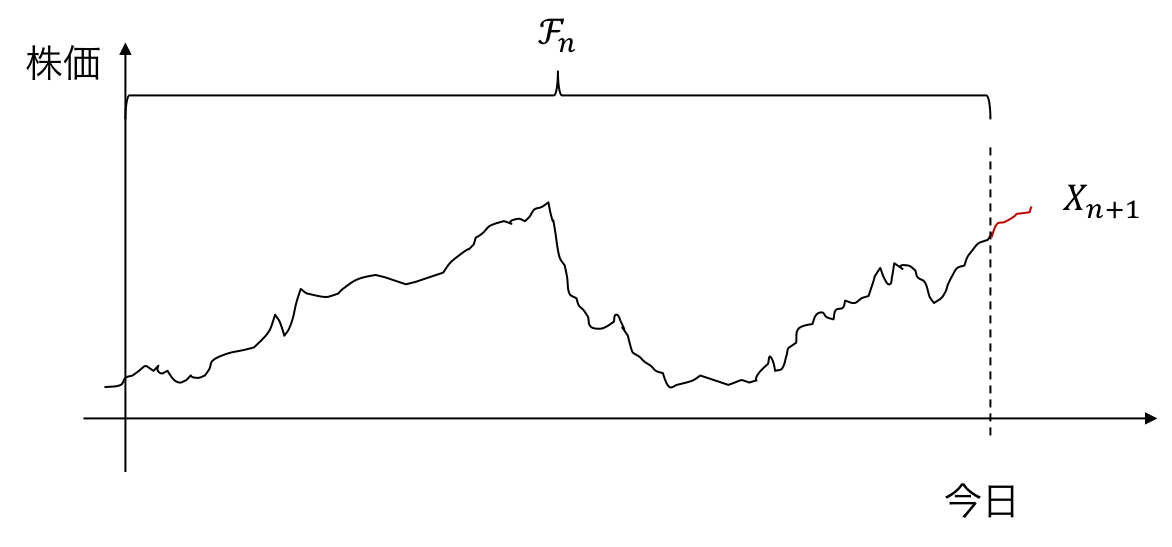
例2: 株価予測¶
今日までの株価データから明日の株価を予測したい
- $z_n=(\mathcal{F}_n, x_{n+1})$
- $x_n$: $n$日目の株価
- $\mathcal{F}_n = \{x_1,x_2,\dots,x_n\}$: $n$日目までの株価
- $p(X_{n+1} \mid \mathcal{F}_n)$ を推定したい
例4: 化学物質生成¶
特定の物性の化学物質を色々生成したい
- $z_n = (x_n, y_n)$:
- $x_n\in\mathcal{G}$ は構造式(グラフ形式)
- $y_n\in\mathcal{P}$ は物性
- 水への溶けやすさ
- 特定のタンパク質への結合しやすさ
- $p(x\mid y)$ を推定したい
例5: データの理解¶
- $z_n=(x_n, y_n)$:
- $x_n$: 観測データ
- $y_n\in\{1,\dots,C\}$: 未観測データ
- $p(x, y)$ を推定したい
- 推定した $y$ を用いてラベルなしでデータを分類できる
まとめ¶
- 様々な問題は確率分布の推定に帰着される
- 主に以下の二種類に分類される
- $p(y \mid x)$ を推定
- $p(x \mid y)$ や $p(x)$ を推定
- $y$より$x$の方が「複雑」とする
機械学習の分類¶
- 教師あり学習 と 教師なし学習 が代表的な2つの問題
- 他にもたくさんの問題があるし、はっきりと分類できるとは限らない
- 半教師あり学習
- 異常検知・変化検知
- 強化学習
- etc.
1. 教師あり学習¶
- 入力: データがペア$(x,y)$で与えられている
- $x$ は簡単に手に入るもの
- $y$ は$x$の属性で、簡単には手に入らないもの
- 人間が見て判断するもの
- 実験で測定した結果
- 明日にならないとわからないこと
- 目的: $p(y \mid x)$ を推定したい
1. 教師あり学習¶
- 利点: 予測結果がわかりやすい
- $y=0$ ならこの画像には猫がいない
- $y=1$ ならこの画像には猫がいる
- 欠点: ラベル付きデータセットを作るコストがかかる
- ImageNet は1400万枚の画像にラベル付けをしている
2. 教師なし学習¶
- 入力: データは$x$のみ
- 目的: $p(x)$ または $p(x, y)$ を推定したい
- $y$ は未観測
2. 教師なし学習¶
- 利点: ラベル付けをしなくてよい
- ラベル付けをしなくてもモデルがラベルを含め学習する
- $x$ と $y$ の関係をモデル化することで可能になる
- 欠点
- ラベルの解釈は人間が行う必要がある
- $y\in\{1,\dots,C\}$ のようにデータを$C$個に分割するが、各分割の意味合いはわからない
- 確率分布の推定が難しいことが多い(後述)
- ラベルの解釈は人間が行う必要がある
ここまでのまとめ¶
- 機械学習の問題は、データセットから確率分布を推定する問題に帰着されることが多い
- 各データが同一の確率分布に従うと仮定
- 有限サイズのサンプルから確率分布を推定
- 教師あり学習と教師なし学習の2つが代表的な問題
- 教師あり学習は教師ラベルが必要
- 教師なし学習は教師ラベルが不要
- 本講義では 教師なし学習 を取り扱います
- 他の講義で教師あり学習を取り扱っている(?)
- 確率分布の推定手法に工夫が必要なことが多い
統計的機械学習の定式化(詳細)¶
具体的にどのように学習を行うのかを説明する
- サンプル: $\mathcal{D} = \{z_n\in\mathcal{Z} \mid n=1,\dots,N\}$
- 仮定: $z_n \overset{\mathrm{iid}}{\sim} p^\star(Z)$ ($p^\star$: 未知の確率分布)
- パラメトリックモデル $\mathcal{M}=\{p(Z ; \theta) \mid \theta\in\Theta\}$ の中から $p^\star$ に近いものをサンプルから推定する
- ふたつの定式化を紹介する
- 最尤推定
- ベイズ推定
定式化1: 最尤推定¶
最も基本的な定式化では、最尤推定を行う。つまり負の対数尤度を
演習¶
- サンプル: $x_1,\dots,x_N\in\mathbb{R}$
- パラメトリックモデル: $\mathcal{M} = \{\mathcal{N}(\mu, 1) \mid \mu\in\mathbb{R}\}$
- $\mathcal{N}(\mu, \sigma^2)$: 平均$\mu$、分散$\sigma^2$の正規分布
- $\mathcal{N}(\mu, \sigma^2)$の確率密度関数は $p(x; \mu, \sigma^2) = \dfrac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\dfrac{(x-\mu)^2}{2\sigma^2}\right)$
としたとき、最尤推定量 $\hat\mu$ を求めよ。
答え¶
$-\log p(x;\mu, 1) = \dfrac{(x-\mu)^2}{2} + C$($C$ は $x, \mu$ によらない定数)なので、 $$\mathcal{L}(\mu; \mathcal{D}) = \sum_{n=1}^{N}\dfrac{(x_n-\mu)^2}{2} + C$$
$$ \begin{align*} \sum_{n=1}^N \dfrac{(x_n - \mu)^2}{2} &= \dfrac{1}{2} \left(N\mu^2 - 2 \mu\sum_{n=1}^{N}x_n + \sum_{n=1}^{N}x_n^2\right)\\ &= \dfrac{N}{2} \left(\mu^2 - 2 \mu \frac{1}{N}\sum_{n=1}^N x_n + \frac{1}{N} \sum_{n=1}^{N} x_n^2\right)\\ &= \dfrac{N}{2} \left(\mu - \frac{1}{N} \sum_{n=1}^N x_n\right)^2 + C \end{align*} $$ 最後の$C$は$\mu$によらない定数
よって $$ \begin{align*} \hat\mu &= \arg\min_{\mu\in\mathbb{R}} \mathcal{L}(\mu; \mathcal{D}) \\ &= \arg\min_{\mu\in\mathbb{R}} \dfrac{N}{2} \left(\mu - \frac{1}{N} \sum_{n=1}^N x_n\right)^2\\ &= \frac{1}{N} \sum_{n=1}^N x_n \end{align*} $$
- 分散一定、平均未知の正規分布の「学習」は、 $\mu$ にサンプル平均 $\hat\mu$ を代入するだけでよい
- $\mu$ は分布の平均に対応するので、それっぽい
- これで学習なのか?→難しい手法でも大体こんなことをやっているだけなので学習と呼んでいいのでは
- $\hat\theta$ が陽に書けることはあまりない
- 数理最適化の技術を使って数値的に $\hat\theta = \arg\min_{\theta\in\Theta}\mathcal{L}(\theta; \mathcal{D})$ を解く
- そもそも $\mathcal{L}(\theta; \mathcal{D})$ を計算するのに莫大な計算量が必要なこともある
- ↑このあたりのことをやります
そもそもなぜ最尤推定?¶
サンプル $\mathcal{D}$ が観測される確率を最大化するようにパラメタを定めるのはそれっぽいけど...
→ 漸近的(サンプルサイズを無限大にしたとき)に良い性質があるからよく使われる
一致性 (consistency)¶
サンプルが $p(z \mid \theta^\star)$ に従うとする ($\theta^\star \in \Theta$)。このときある一定の条件下で、 $$\hat\theta_N \overset{\mathrm{P}}{\rightarrow} \theta^\star$$ つまり、任意の$\epsilon>0$に対して $$\Pr[d(\hat\theta_N, \theta^\star) > \epsilon] \rightarrow 0\ \text{as}\ N\rightarrow\infty$$ が成り立つ。
- サンプル $\mathcal{D}$ が $p^\star$ に従う確率変数だと思うと $\hat\theta_N$ も確率変数
- サンプルのとり方によっては $\hat\theta_N$ が $\theta^\star$ と全然違う値になってしまう
- サンプルサイズ $N$ が大きくなると上記のようなことが起こる確率が $0$ に近づく
- つまり推定量 $\hat\theta_N$ はサンプルサイズが大きくなるに従って $\theta^\star$ に近づく確率が高くなる
漸近的な有効性 (asymptotic efficiency)¶
ある一定の条件下で、サンプルサイズ $N$ が大きくなるに従って、 $$\mathbb{E}[(\hat\theta_N - \theta^\star)^2]$$ が理論的な下限 (Cramér–Rao bound) に収束する。
- $\mathbb{E}[(\hat\theta_N - \theta^\star)^2]$ は推定量 $\hat\theta_N$ の推定誤差
- サンプルを確率変数として考えたときのブレ
- 変なサンプルがきたら $(\hat\theta_N - \theta^\star)^2$ は大きくなる
- Cramér–Rao bound
- 不偏推定量の推定誤差の下限
- 不偏推定量は、 $\mathbb{E}\hat\theta = \theta$ を満たす推定量のこと
- 最尤推定量は漸近的に不偏かつ有効な推定量
最尤推定のまとめ¶
- 機械学習の問題は最尤推定量 $\hat\theta_N$ を計算することに帰着できる
- サンプル $\mathcal{D}$ で陽に書けることもあれば書けないこともある
- 陽に書けない場合は工夫が必要
- 最尤推定量は漸近的によい性質が色々あるため使われる
- 一致性
- 有効性
- etc.
定式化2: ベイズ推定¶
- サンプル: $\mathcal{D} = \{z_n\in\mathcal{Z} \mid n=1,\dots,N\}$
- 仮定: $z_n \overset{\mathrm{iid}}{\sim} p^\star(Z)$ ($p^\star$: 未知の確率分布)
- パラメトリックモデル $\mathcal{M}=\{p(Z \mid \theta) \mid \theta\in\Theta\}$ の中から $p^\star$ に近い$\theta$が欲しい
- 事前分布 $p(\theta)$ を仮定する
- 事前知識を表現する
- 例えば $p(\theta) = \mathcal{N}(\theta; 0, \Sigma)$ とすると、 $\theta$ はあまり大きな値を取らないという事前知識を反映する
- 事前分布は既知のものとする(パラメタも全部知ってるとする)
- 事後分布 $p(\theta \mid \mathcal{D})$ を計算することで上の問題を解く $$p(\theta \mid \mathcal{D}) = \dfrac{p(\mathcal{D} \mid \theta) p(\theta)}{p(\mathcal{D})}$$
事後分布¶
データセットを観測した元でのモデルパラメタの推定を表す
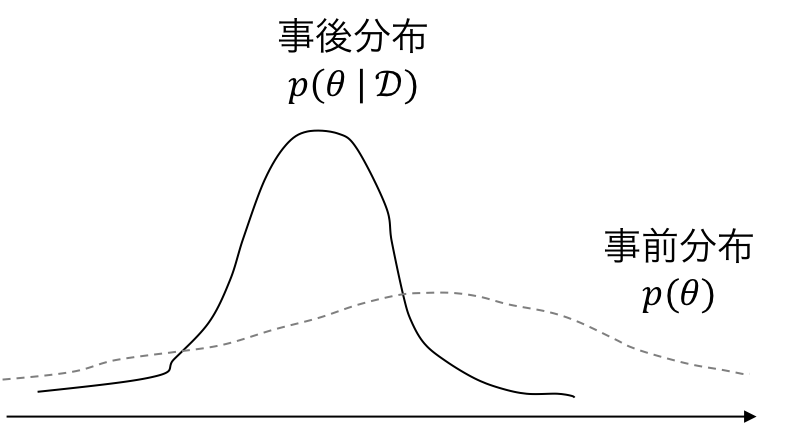
演習¶
- サンプル: $\mathcal{D} = \{x_1,\dots,x_N\}\subset\mathbb{R}$
- パラメトリックモデル: $\mathcal{M} = \{\mathcal{N}(\mu, 1) \mid \mu\in\mathbb{R}\}$
- 事前分布: $p(\mu) = \mathcal{N}(0,1)$
としたとき、 $\mu$ の事後分布 $p(\mu \mid \mathcal{D})$ を求めよ。
答え¶
$$ p(\mu \mid \mathcal{D}) = \dfrac{p(\mathcal{D} \mid \mu)p(\mu)}{p(\mathcal{D})} $$ であるが、 $$ \begin{align} \log (p(\mathcal{D} \mid \mu)p(\mu)) &= \log p(\mathcal{D} \mid \mu) + \log p(\mu) \\ &= \log p(\mu) + \sum_{n=1}^N \log p(x_n \mid \mu)\\ &= - \dfrac{\mu^2}{2} - \sum_{n=1}^N \dfrac{(x_n - \mu)^2}{2} + C \end{align} $$ ($C$は$\mu$に依存しない項)
$$ \begin{align} &= - \dfrac{1}{2}\left((N+1)\mu^2 - 2\mu\sum_{n=1}^{N}x_n + \sum_{n=1}^N x_n^2\right)+C\\ &= - \dfrac{N+1}{2}\left(\mu - \dfrac{1}{N+1}\sum_{n=1}^N x_n\right)^2 +C \end{align} $$
$\log p(\mu\mid \mathcal{D})$ が $\mu$ に関する二次形式なので、 $p(\mu\mid\mathcal{D})$ は正規分布。
- 平均: $\dfrac{1}{N+1}\sum_{n=1}^N x_n$
- 分散: $\dfrac{1}{\sqrt{N+1}}$
ベイズ推定の特徴¶
データセット $\mathcal{D}$ に $x_{N+1}=0$ を加えたような推定値が得られる
- $x_{N+1}=0$ をデータセットに加えると、平均推定は $0$ に近づく
- 事前分布は $\mu$ が $0$ に近いことを仮定していた
ベイズ推定のまとめ¶
- パラメタに対して事前分布 $p(\theta)$ を置く
- 事後分布 $p(\theta \mid \mathcal{D}) = \dfrac{p(\mathcal{D} \mid \theta)p(\theta)}{p(\mathcal{D})}$ を計算する
- またはモデルの中の確率変数 $Z$ に関する事後分布を求めたりもする
- とにかく、データを得た元での興味がある確率変数の事後分布を求める
まとめ (1/2)¶
- 人工知能業界はブームと冬の時代を繰り返してきた
- 直近のブームでは統計的機械学習が注目されている
- 統計的機械学習は、データセットから確率分布を推定する問題を解く
まとめ (2/2)¶
- 教師あり学習と教師なし学習のふたつが機械学習の代表的な問題
- 最尤推定とベイズ推定のふたつが代表的な推定方法
- 教師あり学習をベイズ推定で解いたりするし
- 教師なし学習を最尤推定で解いたりもする
これ以降の授業について¶
- 教師なし学習を主に扱う
- 最尤推定したりベイズ推定したりする
- 推定アルゴリズムの導出
- Python を用いた実装